행렬 분해

행렬분해(matrix factorization)는 널리 알려진 추천 알고리즘으로, "고객님을 위한 추천상품"과 같은 개인화 추천상품 선정을 위한 대표적인 방법이다. 흔히 쓰이는 협업 필터링(collaborative filtering)이라는 용어는 좁은 의미로 쓰일 때에는 행렬 분해방법을 뜻하기도 하지만 일반적으로 다른 추천 알고리즘을 지칭하는 경우도 있다.

입력 데이터

행렬분해 방법에는 구매정보를 이용한다. 예를 들어 좋은서점닷컴의 다음과 같은 구매정보을 생각해보자. 일반적인 구매기록에는 구매시각과 같은 추가적인 정보가 있지만, 행렬분해에서는 누가 어떤 상품을 구매했는지만을 이용한다.

사용자	상품
사용자1	서적1
사용자1	서적3
사용자1	서적7
사용자2	서적2
사용자2	서적4
사용자2	서적6
사용자2	서적8
사용자3	서적3
사용자3	서적7
사용자3	서적9
사용자3	서적10
사용자4	서적2
사용자4	서적5
사용자4	서적6

이 구매정보를 아래와 같이 행렬(matrix)모양으로 표현할 수 있다.

사용자	서적1	서적2	서적3	서적4	서적5	서적6	서적7	서적8	서적9	서적10
사용자1	1	0	1	0	0	0	1	0	0	0
사용자2	0	1	0	1	0	1	0	1	0	0
사용자3	0	0	1	0	0	0	1	0	1	1
사용자4	0	1	0	0	1	1	0	0	0	0

이 행렬에서 가로줄은 사용자를, 세로줄은 상품을 나타낸다. 가로줄에 해당하는 사용자가 세로줄에 해당하는 상품을 구매한 기록이 있으면 해당 항목이 1 그렇지 않으면 0이다. 행렬의 가로줄(row)의 수는 전체 사용자를 나타내는 4이고 세로줄의 수는 전체 상품 수를 나타내는 10이다. 이 행렬을 $M$ 이라고 부르기로 하자.

M = \begin{pmatrix} 1 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 1 & 0 & 1 & 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 & 1 & 0 & 1 & 1 \\ 0 & 1 & 0 & 0 & 1 & 1 & 0 & 0 & 0 & 0 \\ \end{pmatrix}

행렬분해 방법 목적은 행렬 $M$ 에서 아직 구매가 일어나지 않은 항목, 즉, 0으로 표시된 항목 가운데 향후 구매의 가능성이 높은 항목들을 찾는 것이다. 이를 위해서 $M$ 을 두개의 다른 행렬의 행렬곱셈(matrix multiplication)으로 표현할 수 있는 인자들 즉,

FG \approx M

를 만족하는 두 행렬 $F$ 와 $G$ 를 구하게 된다. $FG$ 는 두 행렬 $F$ 와 $G$ 의 행렬곱셉(matrix multiplication)을 나타낸다. 각 행렬의 모양을 살펴보면

$M$ : 가로줄 수는 4, 세로줄 수는 10
$F$ : 가로줄 수는 4, 세로줄 수는 $k$
$G$ : 가로줄 수는 $k$ , 세로줄 수는 10

와 같고 $k$ 는 선택이 가능한 매개변수이다. 행렬 $F$ 의 $i$ 번째 가로줄은 사용자 $i$ 을 나타내는 벡터로 사용자 벡터(user vector)라고 불린다. 행렬 $G$ 의 $j$ 번째 세로줄은 상품 $j$ 를 나타내는 벡터로 상품 벡터 (item vector)라고 불린다. 사용자 벡터 $i$ 와 상품 벡터 $j$ 의 내적(dot product)은 상품 $j$ 가 사용자 $i$ 에게 어느정도 유용한지를 표현하게 된다. 사용자 벡터와 상품 벡터의 길이는 모두 $k$ 이다.

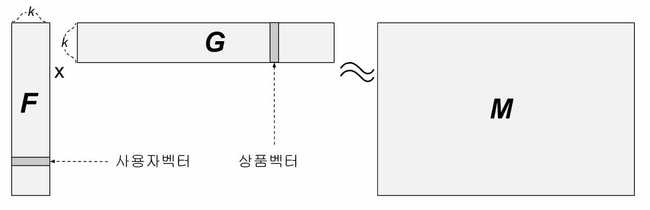
매개변수 $k$ 는 원래 행렬 $M$ 의 가로줄 수나 세로줄 수 보다 작은 값을 선택한다. 예제의 행렬 $M$ 에서 $k$ 는 4와 10보다 작은 값이 필요하므로 가령 $k$ =2를 생각해 볼 수 있겠다. 실제 데이터에서 $M$ 의 가로줄과 세로줄의 수는 각각 사용자의 수와 상품의 수를 나타내므로 수천, 수만, 수십만, 수백만 또는 그 이상이 될 수도 있는 반면, $k$ 는 주로 수십 또는 많아도 수백정도의 범위에서 선택하는 것이 일반적이다. 예를 들어 $M$ 의 가로줄 수가 300,000이고 세로줄 수가 2,000,000 일 때 $k$ =50정도 이므로 $k$ 가 얼마나 작은지 알 수 있다.

		내적(dot product)
사용자1	서적1	0.388
사용자1	서적2	-0.012
사용자1	서적3	0.862
사용자1	서적4	-0.008
사용자1	서적5	-0.001
사용자1	서적6	-0.005
사용자1	서적7	0.871
사용자1	서적8	0.001
사용자1	서적9	0.485
사용자1	서적10	0.481

		동일한 서적을 구입한 숫자
사용자1	사용자2	0권
사용자1	사용자3	2권
사용자1	사용자4	0권

행렬 분해의 학습

행렬분해 방법 학습의 핵심은 $FG \approx M$ 을 최대한으로 만족시키는 $F$ 와 $G$ 를 찾는 것이다. 이를 계산과학의 최적화(optimization)문제로 표현하는데, 가장 간단한 형태는

\min_{F,G} \frac{1}{2} \left|| M - FG \right||_F^2

이지만, 추천 시스템에서는

\min_{F,G} \frac{1}{2} \left( \sum_{M_{ij} = 1} (M_{ij} - (FG)_{ij} )^2 + C_1 \sum_{M_{ij} = 0} (M_{ij} - (FG)_{ij} )^2 \right)

와 같은 표현이 일반적이다. 첫번째와 달리 두번째에서는 "구매하였다"는 정보( $M_{ij} = 1$ )와 "구매하지 않았다"는 정보( $M_{ij} = 0$ )를 다른 중요도로 처리하고, 매개변수 $C_1$ ( $C_1$ >0) 를 이용해 중요도의 차이를 설정한다. 매개변수 $C_1$ 은 1보다 작은 값을 선택하는데, 왜 그런지 직관적으로 생각해 보면 $M_{ij} = 1$ 은 사용자 $i$ 가 상품 $j$ 에 관심이 있다는 분명한 정보를 나타내는 반면 $M_{ij} = 0$ 의 경우 사용자가 $i$ 가 상품 $j$ 에 관심이 없기 때문일 수도 혹은 사용자 $i$ 가 상품 $j$ 에 관심이 있지만 아직 구매할 기회가 없었기 때문일 수도 있기 때문이다.

여기에 행렬 $F$ 와 $G$ 을 구성하는 숫자들이 지나치게 커지는 것을 막기 위해

C_2 \left|| F \right||_F^2 + C_3 \left|| G \right||_F^2

와 같은 항목을 추가하는 경우가 많다. 또한, 입력 행렬 $M_{ij}$ 에 $0$ 또는 $1$ 만 있기 때문에

\min_{F,G} \frac{1}{2} \left( \sum_{M_{ij} = 1} \log \left( \sigma((FG)_{ij}) \right) + C_2 \sum_{M_{ij} = 0} \log \left( 1 - \sigma((FG)_{ij}) \right) \right)

와 같은 최적화문제도 표현하기도 한다.

최적화 문제를 만족하는 두 행렬 $F$ 와 $G$ 를 찾아나가는 과정이 행렬분해의 학습이다. 수학적으로 다양한 방법이 있지만, 확률적 경사 하강법(stochastic gradient descent)이 대표적이다.

희소 행렬 표현

행렬분해의 입력 행렬 $M$ 은 일반적으로 0의 비율이 매우 높다. 예를 들면 좋은서점닷컴의 사용자 수가 $300,000$ 이고 상품 수가 $2,000,000$ 이라고 하면 입력 행렬 $M$ 의 모든 항목 수는 $300,000 \times 2,000,000 = 60,000,000,000$ 가 되는데, 이를 일반적인 형태인 밀집 행렬(dense matrix representation)로 저장하는 것은 컴퓨터의 메모리 용량을 초과하기에 가능하지 않다. 한편, 한 명의 사용자가 구매하는 서적의 수는 그다지 많지 않아서, 가령 좋은서점닷컴의 사용자가 평균 20권을 구매했다고 생각하면 $300,000 \times 20 = 6,000,000$ 만큼의 구매정보가 있는 셈이고 행렬 $M$ 의 나머지 항목들은 모두 0이기 때문에 99.9%이 0이라는 점을 알 수 있다. 이런 행렬은 0을 제외한 항목들의 위치와 값만을 표시하는 희소 행렬(sparse matrix representation)로 표현한다.

행렬 $M$ 의 이같은 특징을 행렬분해의 학습알고리즘에 활용한다. 행렬분해 학습을 위한 확률적 경사 하강법의 단순한 형태는

각 사용자 $i$ 에 대해

각 사용자 $j$ 에 대해

사용자 벡터 $i$ 와 상품 벡터 $j$ 의 내적(dot product)을 $M_{ij}$ 와 비교하여 기울기(gradient) 벡터를 구하고, 이를 바탕으로 사용자 벡터 $i$ 와 상품 벡터 $j$ 를 수정

하는 것이다. 전체 데이터를 한번 사용하는 이 과정을 에폭(epoch)이라고 하고, 주로 수십에서 수백번의 에폭을 반복한 후 학습을 끝낸다. 이를 그대로 행렬 $M$ 에 적용하면 99.9%이상의 학습 시간을 $M_{ij} = 0$ 인 경우에 사용하게 되는데, 실제 구매정보는 $M_{ij} \neq 0$ 인 항목이라는 점을 감안할 때 학습속도가 너무 느려서 사용하기 어렵다. 따라서 $M_{ij} = 0$ 인 항목들은 매 에폭마다 사용하고 $M_{ij} \neq 0$ 인 항목들은 확률적으로 추출해서 사용한다. 매 에폭마다

$M_{ij} \neq 0$ 인 모든 ( $i$ , $j$ )를 이용하여 기울기(gradient) 벡터를 구하고 사용자 벡터 $i$ 와 상품 벡터 $j$ 를 수정
$M_{ij} = 0$ 인 ( $i$ , $j$ )가운데 정해진 개수의 항목을 추출(sample)하여 기울기(gradient) 벡터를 구하고 사용자 벡터 $i$ 와 상품 벡터 $j$ 들을 수정

하는 과정을 거친다. 가령 $M_{ij} \neq 0$ 인 항목과 $M_{ij} = 0$ 인 항목의 비율을 1:1로 유지하는 방법을 생각할 수 있는데 $M_{ij} \neq 0$ 인 항목의 숫자가 6,000,000 라면 $M_{ij} = 0$ 인 항목도 6,000,000 만큼 추출하게 되므로 하나의 에폭에서 12,000,000 개의 $M_{ij}$ 항목을 사용하여 경사 하강(gradient descent)을 실시한다.

여기서 $M_{ij} \neq 0$ 인 항목들은 매번 확률적으로 추출된다는 점을 기억하자. 한 에폭을 마치고 다음 에폭이 되면 $M_{ij} \neq 0$ 인 6,000,000개의 항목은 앞서의 에폭과 동일하지만 $M_{ij} = 0$ 인 6,000,000개의 항목은 새로운 확률 추출과정을 거치기 때문에 앞서와는 다른 항목들이 될 것이다. 이처럼 $M_{ij} = 0$ 인 항목들을 추출하는 것을 네거티브 추출(negative sampling)이라고 한다.

유사 상품 추천

사용자 벡터와 상품 벡터들은 개인화 추천상품 선정이외에도 활용도가 높다. 가령 상품 벡터들 간의 코사인(cosine) 값을 비교하면 유사상품 추천에 사용할 수 있다. 행렬 $G$ 를 사용하여, 서적1을 기준으로 유사상품을 계산하는 예를 들어보자. 서적1의 상품벡터와 다른 상품의 상품벡터간에 코사인 값을 계산해 보면

		상품 벡터간 코사인
서적1	서적2	-0.00679
서적1	서적3	0.99994
서적1	서적4	-0.01051
서적1	서적5	0.00545
서적1	서적6	0.00152
서적1	서적7	0.99996
서적1	서적8	0.00919
서적1	서적9	0.99998
서적1	서적10	0.99956

와 같아서 서적1의 유사상품을 서적9, 서적3, 서적10, 서적7의 순서로 선정할 수 있다.

이밖에도 사용자 벡터들에 K-means와 같은 군집화(clustering) 알고리즘을 적용하면 성향이 비슷한 고객집단을 알아내는데 유용하고, 상품벡터들에 군집화(clustering) 알고리즘을 적용하면 유사한 상품묶음을 알아내는데 쓸모가 있다.

데이터의 종류와 크기

위에서 구매기록을 바탕으로 입력 행렬을 만들었는데, 구매정보외에 장바구니담기, 좋아요, 클릭등 다양한 추가정보를 사용하는 것이 가능하다. 두 가지 이상의 정보를 사용하게 되는 경우 매개변수를 이용해 각 정보의 중요도를 나타낼 수 있다. 가령 구매정보를 이용한 행렬 $M_{구매}$ , 장바구니 담기 정보를 이용한 행렬 $M_{장바구니\ 담기}$ , 클릭 정보를 이용한 행렬 $M_{클릭}$ 을 따로따로 만든 후

M = W_1 \times M_{구매} + W_2 \times M_{장바구니\ 담기} + W_3 \times M_{클릭}

와 같이 표현하고 매개변수 $W_1$ , $W_2$ , $W_3$ ( $W_1, W_2, W_3 > 0$ ) 를 적절히 선택할 수 있다.

구매정보, 장바구니정보, 클릭정보를 비교해 보면 관심사의 정도와 데이터의 크기 면에서 상충관계(trade-off)를 보인다. 관심사의 정도를 기준으로 보면 구매한 서적의 관심도가 가장 높고, 장바구니에 담은 서적은 구매한 경우만큼은 아니지만 여전히 높은 관심도를 나타낸다. 클릭한 서적은 구매나 장바구니에 담은 서적에 비해서는 약한 관심도를 표현한다고 볼 수 있으므로, 매개변수는 $C1 > C2 > C3 > 0$ 이 되는 것이 적절하다. 한편, 데이터의 크기를 기준으로 보면 그 반대의 순서가 된다. 구매정보의 데이터 크기가 가장 작고 그 다음이 장바구니 담기 정보, 클릭 정보의 순서이다. 사용자의 입장에서 생각해 보면, 좋은서점닷컴을 이용하면서 많은 수의 서적을 클릭해서 상세정보를 고려한 후, 관심이 가는 몇개의 서적을 장바구니에 담았다가, 그 중 한 두 권만 구매하게 되기 때문이다.

행렬 분해를 처음 도입할 때에는 구매정보만을 사용하는 것이 가장 쉽다. 데이터의 크기가 작으면 학습과정에서 메모리 관련 문제가 발생할 가능성이 낮고 학습 시간도 짧기 때문이다. 첫 구현을 성공시키고 나서 차후에 장바구니 정보나 클릭정보 등을 포함시켜가면서 좀더 큰 데이터를 학습에 이용하면서 추천시스템을 개선해 나가면 좋다.

학습주기와 연속 학습

인기상품 추천에 관한 첫번째 글에서 갱신 주기에 대해 설명했는데, 행렬 분해에서도 마찬가지로 학습 주기에 대해 고려할 필요가 있다. 가령 매일, 매주, 매 몇시간 마다 학습하는 것을 생각할 수 있다. 한번 학습이 끝나고 나면 다음번 학습 때까지는 사용자 벡터와 상품 벡터가 변하지 않으므로, 학습 주기가 너무 길면 추천 시스템의 사용자 편의성이 저하된다. 자주 학습시키면 좋지만, 너무 짧으면 유지보수에 부담이 되므로 적절히 선택하는 게 좋다.

한번 학습시키는 데 걸리는 시간도 고려한다. 웹사이트의 사용자가 많거나, 상품의 숫자가 많거나, 학습에 사용하는 정보의 크기가 클 수록 학습에 걸리는 시간이 길어진다. 몇 시간정도에 학습을 끝낼 수 있도록 하는게 바람직하고, 길어져서 24시간을 넘어가기 시작하면 주기적으로 학습을 실시해야 하는 시스템에서는 부담이 되기 쉽다. 따라서 웹사이트의 사용자가 많아지거나 학습에 사용하는 정보를 추가하는 경우 학습시간을 개선시키는 노력을 꾀하게 되는데 학습 알고리즘의 개선, 병렬화, 또는 개선된 하드웨어를 사용하는 것 등이 방법이다.

주기적으로 학습시키는 방법의 단점은 학습 데이터가 많을수록 시간이 오래 걸리고 학습 주기 사이에 사용자가 상품을 구매하거나 장바구니에 담더라도 그 정보가 사용자 벡터와 상품 벡터에 반영되지 않는다는 점이다. 이 같은 단점을 피하기 위해 연속 학습으로 시스템을 구성하기도 한다. 연속 학습이란 학습을 멈추지 않고 계속 진행하는 것으로 online learning, continual learning등의 용어로 다양한 연구가 되어 있다. 연속 학습을 구현하는 데에는 그 나름의 어려움이 있는데 대표적으로 신상품이나 생기거나 새 고객이 가입할 때에 상품 벡터와 사용자 벡터를 추가하여 학습을 이어나가야 하고, 마찬가지로 판매가 중단된 상품이나 더이상 활동이 없는 고객에 대한 상품 벡터와 사용자 벡터를 제거해 나가야 한다는 점이 있다. 또한 새로운 정보를 이용하여 학습 할 때 오래된 정보로부터 학습한 내용과 균형을 맞추는 일이 쉽지 않을 수 있다(catastrophic forgetting). 연속학습에서는 학습을 멈추지 않고 진행해야 하는데 시간이 지나 시스템에 문제가 발생할 경우의 대응책을 마련해야 한다.

이번 글에서는 행렬분해 방법의 개념에 대해서 설명하였다. 행렬분해 방법은 선형대수학의 개념에 바탕을 두고 있으면서도 추천시스템에서 활용하고 개선된 방법들이 학계와 업계에서 널리 연구되어 있다. 다양한 최적화문제 표현법등 여기서 다루지 않은 내용이 많이 있다.

카테고리 추천

인공 신경망